Zad. 1. Na odcinku AB obrano punkt P i zbudowano okręgi o średnicach AP i PB. Sieczna AK pierwszego okręgu jest styczna w punkcie C do drugiego okręgu. Prosta CP przecina pierwszy okrąg w punkcie L. Wiedząc, że |AK|=5 i |KC|=25, oblicz pole trójkąta LBP.
Zad. 2. W kwadrat ABCD wpisano trójkąt równoboczny ABE. Prosta CE przecina bok AD w punkcie F. Wiedząc, że |FE|=6, oblicz pole trójkąta FCD.
Zad. 3. Niech M będzie środkiem boku BC kwadratu ABCD, a AH - wysokością trójkąta AMD. Wiedząc, że |HB|=8, oblicz pole kwadratu.
Zad. 4. (wolna amerykanka) Dany jest kwadrat ABCD. Na boku CD obrano punkt F, a na prostej AB - punkt E takie, że trójkąt AEF jest równoboczny. Proste BC i EF przecinają się w punkcie K. Oblicz miarę kąta KAE.
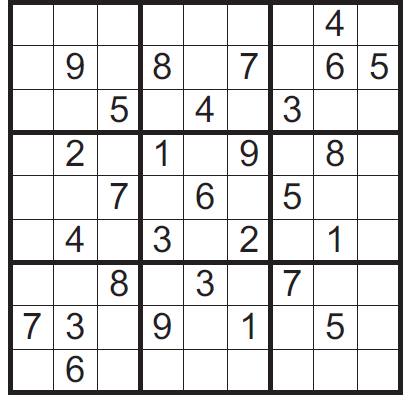
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
